Ya en el siglo XVII existían los concursos científicos. Corría el año 1696 cuando Johann Bernoulli (1) ofreció públicamente, a través de la Royal Society, regalar un valioso libro de su biblioteca personal a aquel que resolviese un par de problemas matemáticos sobre geometría de curvas, que pasarían a conocerse como problemas de la braquistócrona y la cicloide (2). Concedió un plazo de seis meses.
Finalizado el plazo, únicamente uno de los problemas había sido resuelto, nada más y nada menos que por Gottfried Leibniz. A pesar de ser unos de los gigantes matemáticos del momento, su resolución no era demasiado elegante. De todos modos, las bases del concurso establecían que el ganador debía resolver ambos, de modo que Bernoulli declaró el concurso desierto y decidió extender el plazo otros seis meses más… sin lograr ningún éxito adicional.

Representaciones gráficas en coordenadas polares de la ecuación r=sin(θ*n/d) para varios valores de n y d
A comienzos de 1697 Bernoulli recibió una carta anónima. Contenía dos elegantísimas soluciones para cada uno de los problemas propuestos, pero ninguna firma. Las palabras, quizá apócrifas, que pronunció Bernoulli aquel día, han pasado a los anales de la historia de la ciencia: «Es Newton, reconozco las garras del león».
Sucede además que Newton, por algún motivo, no había sido informado de ninguna de las convocatorias de este concurso, en el que tuvo competidores de la talla de Leibniz, Huygens o L´Hôpital. Fue su colega Edmund Halley quién le invitó a participar. Menos de 24 horas le bastaron para dar con la respuesta de ambos problemas.
Y es que, en matemáticas, al igual que en las bellas artes, también hay aficionados, artesanos de segunda, artesanos de primera y maestros. Del mismo modo que el ojo bien entrenado puede distinguir sin duda alguna la diferencia de estilos entre un Picasso y un Dalí, las matemáticas de los grandes maestros también tienen un toque personal, en ocasiones fortísimo. Además, en este caso, el asunto va mucho más allá de lo estético, pues por lo general hablamos de diferentes modos de abordar un mismo problema.
En este sentido se cuenta una curiosa anécdota protagonizada por John von Neumann, pero permitidme aprovechar para introducir al segundo protagonista de esta historia, el problema de la mosca y los trenes:
Imaginemos dos trenes moviéndose el uno hacia el otro a 10 km/h cada uno, separados inicialmente por 100 km. Imaginemos además una mosca que, partiendo de uno de los trenes, vuela a 20 km/h hacia el otro… y tan pronto como lo toca, da la vuelta y vuelve, una vez más a 20 km/h, hacia el tren inicial… y así una y otra vez. La pregunta es: ¿qué distancia ha volado la mosca en total?
Existe un modo muy sencillo de resolverlo, una especie de truco ingenioso para evitar enredarse en tediosos cálculos: si ambos trenes se mueven a 10 km/h tardarán 5 horas en recorrer los 100 km que les separan. Si la mosca se mueve a 20 km/h durante 5 horas, habrá recorrido finalmente una distancia de 100 km. ¿Fácil, verdad?
Se trata de un problema curioso y de gran valor pedagógico, pues contiene dos detalles intuitivos que, en conjunto, son muy interesantes: por un lado, la mosca recorre una distancia finita (100 km) y por el otro, sin embargo, la mosca hace un número infinito de viajes cada vez más cortos. A menudo se pone este ejemplo a los estudiantes que se sienten incómodos con la idea de que una suma con infinitos términos pueda tener un resultado finito.
La anécdota atribuida a von Neumann, consiste en que al parecer en cierta ocasión se le propuso este problema durante una celebración, en un entorno relajado. Sin apenas pestañear, dio la respuesta adecuada. Alguien comentó que von Neumann se había percatado del truco… pero von Neumann preguntó: «¿qué truco?». El genio húngaro, muy fiel a su estilo, había planteado y sumado la serie infinita sin necesidad de papel ni lápiz.
Otro ejemplo, bien conocido por los estudiantes, es el de las dos notaciones más populares para el concepto de derivada:
En un primer vistazo son enteramente equivalentes, pues ambas representan la misma idea: derivada. Sin embargo, el uso de unas u otras levanta encendidas y apasionadísimas discusiones, especialmente entre los estudiantes. Lo sorprendente es que el uso de una u otra puede hacer más fácil la resolución de ciertos problemas. Por ejemplo, la notación fraccionaria (también llamada notación de Leibniz) posee ventajas evidentes en problemas que exigen utilizar la regla de la cadena, o trabajar con más de una variable independiente.
Incluso los artesanos de segunda, como el que suscribe, tenemos nuestro estilo propio y, sobretodo, nuestras preferencias personales. Existen autores claros y didácticos, y también auténticos Góngoras de las matemáticas. Incluso ha habido corrientes entre los matemáticos que podríamos llamar estéticas, siendo las dos principales las de los formalistas, partidarios de la lógica más árida e indiscutible, y los intuicionistas, partidarios de un uso más extensivo de las metáforas y la intuición.
Las matemáticas, lejos de ser esa rama fría, técnica y aburrida que a menudo nos hacen creer en nuestros primeros años como estudiantes y que persuade a la mayoría de continuar estudiándolas, tienen mucho más de arte de lo que se suele imaginar.
Notas:
(1) Los Bernoulli eran una auténtica dinastía de físicos y matemáticos de origen suizo. Hasta 9 de sus miembros se dedicaron a la física o las matemáticas, alcanzando algunos de ellos el Olimpo de los libros de historia de la ciencia.
(2) A menudo se llama a la cicloide, por su belleza y elegancia, la Helena de la Geometría, en referencia a Helena de Troya.
Referencias:
George Finlay Simmons. Calculus gems. Brief lives and memorable mathematics. McGraw-Hill, 1992.

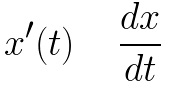
Si los trenes se mueven uno hacia el otro y la velocidad es de 10 Km/hora, en 5 horas recorren 50 km cada uno y se encuentran. En el razonamiento del problema pareciera que dicen que cada tren recorre 100 km, en realidad cada tren recorre solamente 50 km